Гидравлические потери (общие сведения) Потери удельной энергии (напора), или, как их часто называют, гидравлические потери, зависят от формы, размеров русла, скорости течения и вязкости жидкости, а иногда и от абсолютного давления в ней. Вязкость жидкости, хотя и является первопричиной всех гидравлических потерь, но далеко не всегда оказывает существенное влияние на их величину.
Как показывают опыты, во многих, но не во всех случаях гидравлические потери приблизительно пропорциональны скорости течения жидкости во второй степени, поэтому в гидравлике принят следующий общий способ выражения гидравлических потерь полного напора в линейных единицах:
...
Читать дальше »
|
Уравнение Бернулли для потока реальной (вязкой) жидкости При переходе от элементарной струйки идеальной жидкости к потоку реальной (вязкой) жидкости, имеющему конечные размеры и ограниченному стенками, необходимо учесть неравномерность распределения скоростей по сечению, а также потери энергии (напора). То и другое является следствием вязкости жидкости.
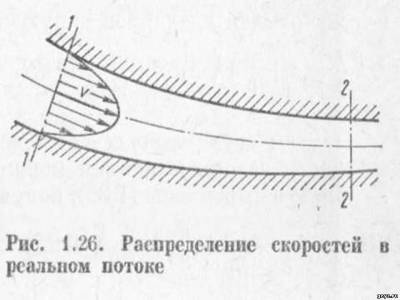
При движении вязкой жидкости вдол
...
Читать дальше »
|
Вывод дифференциальных уравнений движения идеальной жидкости и их интегрирование 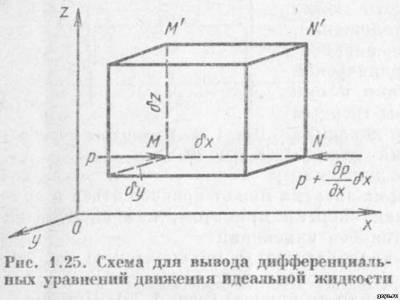 В потоке идеальной жидкости возьмем произвольную точку М с координатами х, у, z (рис. 1.25) и выделим у этой точки элемент жидкости в форме прямоугольного параллелепипеда так, чтобы точка М была бы одной из его вершин. Пусть ребра этого параллелепипеда будут параллельны координатным осям и соответственно равны 8х, б у и
...
Читать дальше » В потоке идеальной жидкости возьмем произвольную точку М с координатами х, у, z (рис. 1.25) и выделим у этой точки элемент жидкости в форме прямоугольного параллелепипеда так, чтобы точка М была бы одной из его вершин. Пусть ребра этого параллелепипеда будут параллельны координатным осям и соответственно равны 8х, б у и
...
Читать дальше »
|
Уравнение Бернулли для элементарной струйки идеальной жидкости Рассмотрим установившееся течение идеальной жидкости, находящейся под действием лишь одной массовой силы — силы тяжести, и выведем для этого случая основное уравнение, связывающее между собой давление в жидкости и скорость ее движения.
Возьмем одну из элементарных струек, составляющих поток, п выделим сечениями 1 и 2 участок этой струйки произвольной длины (рис. 1.22). Пусть площадь первого сечения равна dSv скорость внем vv давление plf а высота расположения центра тяжести сечения, отсчитанная от произвольной горизонтальной плоскости сравнения, zv Во втором сечении соответственно dS2, и2, р2 и z
...
Читать дальше »
|
Расход. Уравнение расхода Расходом называется количество жидкости, протекающее через живое течение потока (струйки) в единицу времени. Это количество можно измерить в единицах объема, в весовых единицах или в единицах массы, в связи с чем различают объемный Q, весовой Qq и массовый Qm расходы.
Для элементарной струйки, имеющей бесконечно малые площади сечений, можно считать истинную скорость v одинаковой во всех точках каждого сечения.
- Следовательно, для этой струйки объемный
- Для потока конечных размеров в общем случае скорость имеет различное значение в разных точках сечения, поэтому расход надо определять как сумму элементарн
...
Читать дальше »
|
Основные понятия Кинематика жидкости существенно отличается от кинематики твердого тела. Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют; эта среда состоит из множества частиц, движущихся одна относительно другой.
Скорость в данной точке пространства, занятого движущейся жидкостью, является функцией координат этой точки, а иногда и времени. Таким образом, задачей кинематики жидкости является определение скорости в любой точке жидкой среды, т. е. нахождение поля скоростей.
Сначала рассмотрим движение так называемой идеальной жидкости, т. е. такой воображаемой жидкости, кото
...
Читать дальше »
|
Равномерное вращение сосуда с жидкостью Возьмем открытый цилиндрический сосуд с жидкостью и сообщим ему вращение с постоянной угловой скоростью со вокруг его вертикальной оси. Жидкость постепенно приобретет ту же угловую скорость, что и сосуд, а свободная поверхность ее видоизменится; в центральной части уровень жидкости понизится, у стенок — повысится, и вся свободная поверхность жидкости станет некоторой поверхностью вращения (рис. 1.18).
На жидкость в этом случае будут действовать две массовые силы — сила тяжести и центробежная сила, которые, будучи отнесенными к единице массы, соответственно равны g и со2г.
Равнодействующая массовая сила j увеличи
...
Читать дальше »
|
Прямолинейное равноускоренное движение сосуда с жидкостью Ранее было рассмотрено в основном равновесие жидкости под действием лишь одной массовой силы — ее веса. Этот случай имеет место тогда, когда жидкость покоится в сосуде, неподвижном относительно Земли, а также в сосуде, движущемся равномерно и прямолинейно. Если же сосуд с жидкостью находится в неравномерном или непрямолинейном движении, то на частицы жидкости кроме силы тяжести действуют еще силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.
При относительном покое свободная поверхность жидкос
...
Читать дальше »
|
Сила давления жидкости на криволинейные стенки.
Плавание тел. Нахождение силы давления жидкости на поверхности произвольной формы в общем случае приводится к определению трех составляющих суммарной силы и трех моментов. Чаще всего рассматривают цилиндрические или сферические поверхности, имеющие вертикальную плоскость симметрии. Сила давления жидкости в этом случае сводится к равнодействующей силе, лежащей в плоскости симметрии.
Возьмем цилиндрическую поверхность АВ с образующей, перпендикулярной к плоскости чертежа (рис. 1.15), и определим силу давления жидкости на эту поверхность в двух случаях; 1) жидкость расположена сверху (рис. 1.15, а); 2) жидк
...
Читать дальше »
|
Сила давления жидкости на плоскую стенку Используем основное уравнение гидростатики (1.20) для нахождения полной силы давления жидкости на плоскую стенку, наклоненную к горизонту под произвольным углом а (рис. 1.13). Вычислим силу F давления, действующую со стороны жидкости на некоторый участок рассматриваемой стенки, ограниченный произвольным контуром и имеющий площадь, равную S.
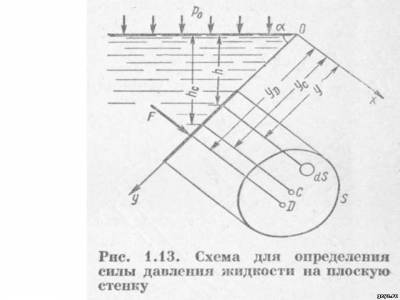
Ось О
...
Читать дальше »
|
|









